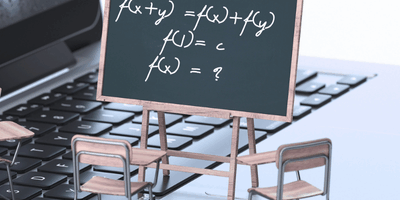Übersicht
Kein Kurs am 03.02. wegen Zeugnisferien.
Der Kurs findet jeden Dienstag an dem auch Schule ist von 17:30 – 18:30 Uhr statt.
Ab 24.2. gibt es einen neuen Link zum Meeting: Hier ist der Link zum Meeting.
Bei Fragen oder sonstigen Anliegen, meldet euch gerne bei mir per Mail: scherer@math.uni-kiel.de oder telefonisch unter 0431 880-5516.
Hast du Interesse an Mathematik und möchtest wissen, was in einer Mathevorlesung an der Uni wirklich passiert?
Oder hast du einfach Spaß an kniffligen Rätseln und klaren, logisch aufgebauten Beweisen? Vielleicht hast du auch ein spannendes Video zu einem Mathe-Thema gesehen, das du so aus der Schule noch gar nicht kanntest, und willst nun tiefer eintauchen?
Dann bist du im Kurs Reine Mathematik genau richtig!
In diesem Kurs beschäftigen wir uns mit interessanten Themen aus vielen verschiedenen Teilgebieten der reinen Mathematik, weit über den Schulstoff hinaus. Eine besondere Stärke der Mathematik ist es, dass man mit wenigen Grundideen schon schöne und elegante Beweise finden kann, und dabei beliebig tief in ein Thema eintauchen kann. Oft stößt man dabei sogar schnell auf ungelöste Fragen!
Im Mittelpunkt stehen dabei anschauliche Konzepte, schöne Beweise und spannende Resultate. Natürlich ist auch Platz für eure eigenen Themenvorschläge und Fragen. In diesem Schuljahr wollen wir uns mit dem Thema Unendlichkeit beschäftigen. Wir werden sehen, dass es unterschiedliche Arten von unendlich gibt, uns mit Folgen und Reihen beschäftigen und die Welt der unendlich dimensionalen Vektorräume entdecken.
Der Kurs richtet sich an alle Schülerinnen und Schüler der 10. bis 13. Klasse, die Lust haben, sich mit etwas abstrakterer Mathematik zu beschäftigen. Voraussetzungen gibt es keine. Der Kurs wird flexibel gestaltet. Ich passe Themen, Schwierigkeitsgrad und Tempo an eure Interessen an. Falls du bestimmte Wünsche, Ideen oder Fragen hast, gibt es dafür natürlich Platz!
Wenn du regelmäßig teilnehmen möchtest, melde dich gerne hier an: Anmeldeformular .
Falls du dir noch nicht sicher bist, schau einfach mal spontan vorbei, eine Anmeldung ist zum Reinschnuppern nicht nötig. Ein Einstieg während des Schuljahres ist auch möglich.
Ich freue mich auf euch!
Kursmerkmale
- Abschnitte 4
- Quiz 1
- Dauer Lebenslanger Zugang
- Klasse(n) Alle Stufen
- Sprache Englisch
- Studierende 8
- Zertifikat Nein
- Einschätzungen Ja
Lehrplan
Lehrplan
- 4 Sections
- 4 Lessons
- unbegrenzt
- Topologie - Juni/Juli 2025Stell dir vor du hast ein geometrisches Objekt. Vielleicht eine Sphäre oder einen Torus, eine Bowlingkugel oder einen Donut. Du darfst das Objekt belienig verformen, verdrehen, strecken, stauchen.Nur zerschneiden oder zerreißen ist nicht erlaubt. Welche Eigenschaften bleiben nun erhalten? Welche Aussagen können wir jetzt noch über das Objekt treffen? Im Juni 2025 beschäftigen wir uns mit Topologie. Das ist ein ziemlich abstrakter Bereich der Mathematik, bei dem es genau um das oben beschriebene Szenario geht. Wir beschäftigen und mit topologischen Räumen. Diese sind ein sehr allgemeines Konzept in der Mathematik und kommen ohne einen Abstandsbegriff aus. Wir sehen wie man Stetigkeit ohne Abstandsbegriff definiert und schauen uns an, wie uns die Gruppentheorie dabei helfen kann rauszufinden, ob zwei topologische Räume gleich sein können, Stichwort Fundamentalgruppen.1
- Unendlichkeit und Mengen - September 2025„Die Anzahl aller natürlichen Zahlen“ ist offensichtlich unendlich, ebenso wie „die Anzahl aller Punkte auf einer Geraden“. Aber lässt sich über solche Zahlen noch etwas anderes sagen, außer dass sie unendlich sind? Oder ist es zum Beispiel möglich, zwei verschiedene Unendlichkeiten miteinander zu vergleichen und festzustellen, welche „größer“ ist? Gibt es überhaupt einen Sinn in der Frage: „Ist die Anzahl aller natürlichen Zahlen größer oder kleiner als die Anzahl aller Punkte auf einer Geraden?“ Solche Fragen, wurden erstmals von dem berühmten Mathematiker Georg Cantor untersucht. In den ersten Wochen des Kurses werden wir uns nun damit beschäftigen.1
- Differentialrechnung - November/Dezember 20252
- Approximationstheorie1